Ahora viene la clase que maneja todo lo que tiene que ver con el gusano, como es: sus movimientos, métodos para ver si se hizo clic en su cabeza o cuerpo, etc. Lo mas difícil ante todo sera hacer crecer al gusano hasta una longitud máxima, regular sus movimientos y darle la capacidad para saltear obstáculos.
4.1. Growing a Worm
El gusano crece almacenando una serie de objectos Point en un array cells[]. Cada punto representa el lugar de uno de los círculos negros del cuerpo del gusano. Emulamos el movimiento colocando una nuevo punto al frente y eliminando la cola (si se debe eliminar). Asi al eliminar la cola tenemos espacio en cells[] y donde podremos agregar una nueva cabeza
Deben recordar uno de los conceptos de programación que siempre nos enseñan, las colas, y su principio básico FIFO, un dibujo para que entiendan:
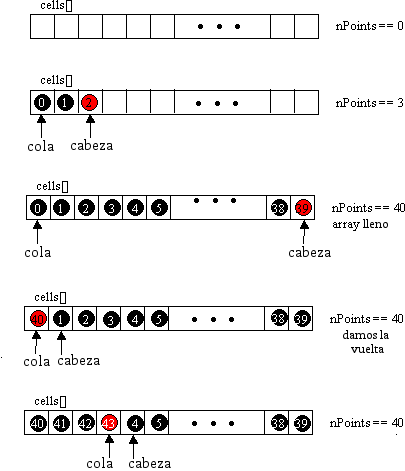
Solo que al momento de salir el que se encuentra en la posición 0 es reemplazado por el de la posición 40 y así sucesivamente.
Los círculos numerados negros y el rojo representan los objetos Point que guardan las coordenadas ( X, Y) de las partes del gusano
La estructura de datos se define así:
private static final int MAXPOINTS = 40; private Point cells[]; private int nPoints; private int tailPosn, headPosn; // La cola y la cabeza del buffer - - - cells = new Point[MAXPOINTS]; // inicializa el buffer nPoints = 0; headPosn = -1; tailPosn = -1;
Otra estructura de datos importante es la ruta actual, la cual puede tener 1 de 8 direcciones predefinidas, desde norte hasta nor-oeste
Cada punto cardinal es representado por un numero:
// las contantes q emulan la direccion/rumbo de un compas private static final int NUM_DIRS = 8; private static final int N = 0; // norte, etc en forma de reloj private static final int NE = 1; private static final int E = 2; private static final int SE = 3; private static final int S = 4; private static final int SW = 5; private static final int W = 6; private static final int NW = 7; private int currCompass; // guarda en la brujula actual la direccion/rumbo
Ahora limitaremos las posibles direcciones que el gusano se puede mover, declarando movimiento predefinidos.
Cuando una cabeza se pinta se coloca en una de las 8 posiciones predefinidas: Norte(0,-1), Sur(0,1), etc.
Los offsets son objetos Point2D.Double, y son guardados en un array incrs[]:
Point2D.Double incrs[];//define la poscion (x,y) en double
-
-
-
// incrementa por cada direccion del compas
incrs = new Point2D.Double[NUM_DIRS];
incrs[N] = new Point2D.Double(0.0, -1.0);//incrs[0]
incrs[NE] = new Point2D.Double(0.7, -0.7);
incrs[E] = new Point2D.Double(1.0, 0.0);
incrs[SE] = new Point2D.Double(0.7, 0.7);
incrs[S] = new Point2D.Double(0.0, 1.0);
incrs[SW] = new Point2D.Double(-0.7, 0.7);
incrs[W] = new Point2D.Double(-1.0, 0.0);
incrs[NW] = new Point2D.Double(-0.7, -0.7);
4.2. Calculating a New Head Point
nextPoint() emplea la posición almacenada en cells[] de la actual cabeza (prevPosn) y la ruta elegida (N, SE), con estos datos calcula el punto para la nueva cabeza
Debemos tener en cuenta que el gusano al llegar abajo debe comenzar arriba y lo mismo pasa en la derecha/izquierda
private Point nextPoint(int prevPosn, int bearing)
/* Retorna la proxima coordenada basado en la posicion
* previa y el rumbo de la brujula
*
* Convertir el rumbo del compas en incrementos predeterminados
* (guardados en incrs[]). Adhiere el incremento multiplicado por
* DOTSIZE de la vieja posicion de la cabeza
*/
{
// consigue el incremento para el rumbo
Point2D.Double incr = incrs[bearing];
int newX = cells[prevPosn].x + (int)(DOTSIZE * incr.x);//el valor x de cells + el valor de incrs[bearing]
int newY = cells[prevPosn].y + (int)(DOTSIZE * incr.y);
// modifica newX/newY si < 0, 0 > pWidth/pHeight;
if (newX+DOTSIZE < 0) // llegamos al borde de la derecha?
newX = newX + pWidth;
else if (newX > pWidth)
newX = newX - pWidth;
if (newY+DOTSIZE < 0) // llegamos al borde de abajo?
newY = newY + pHeight;
else if (newY > pHeight)
newY = newY - pHeight;
return new Point(newX,newY);
} // fin de nextPoint()
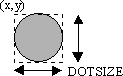
La constante DOTSIZE (12) es la longitud y altura en pixeles del circulo que representa una parte del gusano. La nueva coordenada (newX,newY) es obtenida a partir de incr[]
Cada circulo es definido por su coordenada (x,y) y su longitud DOTSIZE. (x, y) no esta en el centro sino en la esquina izquierda de arriba y se usa para poder pintar el circulo con la función fillOval()
4.3. Choosing a Bearing
la ruta usada proviene de varybearing() que esta definido así:
private int varyBearing()
// variacion del rumbo de la brujula semi-random
{
int newOffset = probsForOffset[ (int)( Math.random()*NUM_PROBS )];
return calcBearing( newOffset );
} // fin de varyBearing()
El array probsForOffset[] es accesado en forma random y devuelve el nuevo offset
private int probsForOffset[]; probsForOffset = new int[NUM_PROBS]; probsForOffset[0] = 0; probsForOffset[1] = 0; probsForOffset[2] = 0; probsForOffset[3] = 1; probsForOffset[4] = 1; probsForOffset[5] = 2; probsForOffset[6] = -1; probsForOffset[7] = -1; probsForOffset[8] = -2;
Si vemos con profundidad este array vemos que el numero que mas se repite es 0 lo que significa que el gusano no variara mucho de dirección, si ponemos 1 o -1 variara un poco mas pero las repeticiones son menores y mucho menos es 2 y -2
y con estos datos podemos usar la función calcBearing()
private int calcBearing(int offset)
// Usa la distancia para calcular un nuevo rumbo del compas
// basado en la direccion actual del compas
{
int turn = currCompass + offset;
//asegurarse que el mov este entre N y NO (0 a 7)
if (turn >= NUM_DIRS)
turn = turn - NUM_DIRS;
else if (turn < 0)
turn = NUM_DIRS + turn;
return turn;
} // fin de calcBearing()
4.4. Dealing With Obstacles
newHead() genera una nueva cabeza usando varyBearing() y nextPoint(), actualizando cell[]
private void newHead(int prevPosn)
/* Crea la nueva posicion de la cabeza y la direccion/rumbo de la brujula
*
* Este tiene 2 partes principales. Primero trataremos de generar una cabeza
* verificando la direccion/rumbo antigua. Pero que pasa si la cbeza choca con un
* obstaculo? entonces cambiamos a la sgte fase
*
* En la segunda fase estamos tratando con una cabeza la cual esta a
* 90 grados en sentido horario, 90 grados en sentido antihorario, o
* 180 grados(toda la vuelta) para que el obstaculo puede ser
* evadido. Estos rumbos son almacenados en fixedOffs[]
*/
{
int fixedOffs[] = {-2, 2, -4}; // distancia para evadir un obstaculo
int newBearing = varyBearing();
Point newPt = nextPoint(prevPosn, newBearing );
//consigue una nueva posicion basado en una variacion
// semi-random de la posicion actual
if (obs.hits(newPt, DOTSIZE)) {
for (int i=0; i < fixedOffs.length; i++) {
newBearing = calcBearing(fixedOffs[i]);
newPt = nextPoint(prevPosn, newBearing);
if (!obs.hits(newPt, DOTSIZE))
break; // una de la distancias arregladas funcionara
}
}
cells[headPosn] = newPt; // nueva posicionde la cabeza
currCompass = newBearing; // nueva direccion de la brujula
} // fin de newHead()
Aca vemos como el gusano lidia con los obstáculos que le vamos poniendo, una de las claves de esta estrategia es asumir que el gusano siempre pueda dar la vuelta, esto se da ya que un jugador no puede poner una caja atrás del gusano ya que lo que habrá es el cuerpo del gusano
4.5. Moving the Worm
El método publico move() inicializa el movimiento del gusano, utilizando newHead() para obtener una nueva posicion de la cabeza y una ruta
El array cells[], tailPosn, headPosn y el numero de puntos en cells[] son actualizados dependiendo del estado en el que se encuentre el gusano, los estados son:
- cuando el gusano se crea
- cuando el gusano crece pero cells[] no esta lleno
- cuando cells[] esta lleno y debemos poner la nueva cabeza en la cola
public void move()
/* Un movimiento causa la adiccion de un nuevo punto al frente del gusano
* que se convierte en la nueva cabeza. Un punto tiene una posicion y una
* direccion/rumbo de la brujula(compas), que se deriva de la posicion de
* la vieja cabeza
*
* move() se complica porque tiene que liar con 3 casos:
* 1) cuando el gusano se crea
* 2) cuando el gusano crece
* 3) Cuando el gusano alcanza la longitud MAXPOINTS (Entonces la adición de una
* cabeza debe ser balanceada removiendo el punto de la cola)
*/
{
int prevPosn = headPosn; // graba la antigua posicion de la cabeza antes de crear una nueva
headPosn = (headPosn + 1) % MAXPOINTS;
if (nPoints == 0) { // una array vacioi al inicio
tailPosn = headPosn;
currCompass = (int)( Math.random()*NUM_DIRS ); // direccion random.
cells[headPosn] = new Point( pWidth/2, pHeight/2 ); // centra pt
nPoints++;
}
else if (nPoints == MAXPOINTS) { // array lleno
tailPosn = (tailPosn + 1) % MAXPOINTS; // olvidate de la antigua cola
newHead(prevPosn);
}
else { // todavia hay espacio en cells[]
newHead(prevPosn);
nPoints++;
}
} // fin de move()
4.6. Drawing the Worm
WormPanel llama al método draw() de Worm
public void draw(Graphics g)
//dibuja un gusano negro con una cabeza roja
{
if (nPoints > 0) {
g.setColor(Color.black);
int i = tailPosn;
while (i != headPosn) {
g.fillOval(cells[i].x, cells[i].y, DOTSIZE, DOTSIZE);
i = (i+1) % MAXPOINTS;
}
g.setColor(Color.red);
g.fillOval( cells[headPosn].x, cells[headPosn].y, DOTSIZE, DOTSIZE);
}
} // fin de draw()
4.7. Testing the Worm
nearHead() y touchedAt() son métodos booleanos usados en WormPanel. nearHead(), estos deciden si las coordenadas están cerca de la cabeza o si touchedAt() esta en el cuerpo del gusano
public boolean nearHead(int x, int y)
// Es (x,y) cerca de la cabeza del gusano?
{ if (nPoints > 0) {
if( (Math.abs( cells[headPosn].x + RADIUS - x) <= DOTSIZE) &&
(Math.abs( cells[headPosn].y + RADIUS - y) <= DOTSIZE) )
return true;
}
return false;
} // fin de nearHead()
public boolean touchedAt(int x, int y)
// Es (x,y) de alguna parte del cuerpo del gusano?
{
int i = tailPosn;
while (i != headPosn) {
if( (Math.abs( cells[i].x + RADIUS - x) <= RADIUS) &&
(Math.abs( cells[i].y + RADIUS - y) <= RADIUS) )
return true;
i = (i+1) % MAXPOINTS;
}
return false;
} // fin de touchedAt()
La constante RADIUS es la mitad del valor de DOTSIZE. nearHead() permite que (x,y) se encuentren dentro de los radios del centro de la cabeza del gusano. touchedAt() chequea por una intersección dentro de un solo radio del centro.
